Кеңістікте Oxyz декарттық координаталар системасы берілсін. M0(x0,y0,z0) нүктесі мен N={A,B,C} векторы берілген болсын. Мынадай теңдеуді қарастыралық:
A(x-x0)+B(y-y0)+C(z-z0)=0 (1)
Бұл теңдеу M0(x0,y0,z0) нүктесі арқылы өтетін, N={A,B,C} векторына перпендикуляр жазықтықты анықтайды. Осы теңдеудегі жақшаларды ашсақ Ax+By+Cz-(Ax0+By0+Cz0)=0 аламыз. Соңғы теңдеудегі жақшадағы санды
-D деп белгілесек жазықтықтың теңдеуі мынадай түрде жазылады:
Ax+By+Cz+D=0. (2)
(2) теңдеу жазықтықтың жалпы теңдеуі деп аталынады. N={A,B,C} векторын жазықтықтың нормаль векторы деп атайды.
Егер жазықтықтың жалпы теңдеуіндегі коэффициенттер нольден ерекше болса, онда теңдеуді – D санына бөліп, теңдеуді мына түрге келтіруге болады:
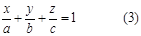
Мұнда a=-D/A, b=-D/B, c=-D/C. Бұл теңдеуді жазықтықтың кесінділік теңдеуі деп айтады. Мұндағы а, b, с сандары жазықтықтың сәйкес абсцисса, ордината, аппликата осьтерінен қиятын кесінділердің ұзындықтары.
Бізге П1, П2 жазықтықтары берілсін:
A1x+B1y+C1z+D1=0 , A2x+B2y+C2z+D2=0 (4)
онда бұл жазықтықтардың қиылысуынан шыққан екі жақты бұрыштардың біреуі осы жазықтардың нормаль векторларының арасындағы бұрышқа тең болады, сондықтан ол бұрышты төмендегі формула арқылы есептеуге болады:
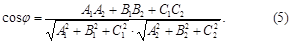
Егер П1, П2 жазықтықтары өзара параллель болса олардың нормаль векторлары коллинеар болады және керісінше де дұрыс. Сондықтан:
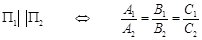
Бұл екі жазықтықтың параллельдік белгісі болады.
Егер П1, П2 жазықтықтары өзара перпендикуляр болса, олардың нормаль векторлары да перпендикуляр болады, демек олардың скалярлық көбейтіндісі нольге тең, яғни:
A1A2+B1B2+C1C2=0.
Толығырақ: https://studopedia.info/4-89182.html
Бұл екі жазықтықтың перпендикулярлық белгісі.