Question

Дөңес төртбұрыштың диагоналі оны төрт үшбұрышқа бөледі. Қарама қарсы орналасқан екі үшбұрыштың аудандарының көбейтіндісі, басқа екі үшбұрыштың аудандарының көбейтіндісіне тең болатынын дәлелдеу керек.

Answer 1

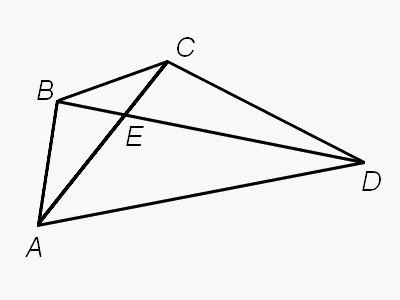
Дөңес төртбұрыштың диагоналдары Е нүктесінде кездессін.

Лемма: S(△AED) : S(△AEB) = DE : BE;

Дәләлі: S(△AED) = AE * ED * sin(∠AED) / 2;
S(△AEB) = AE * EB * sin(∠ARB) / 2;
S(△AED) : S(△AEB) = DE : BE;

Дәл осылай, S(△DEC) : S(△CEB) = DE : BE;

S(△AED) : S(△AEB) = S(△DEC) : S(△CEB) ;

S(△AED) * S(△CEB) = S(△AEB) * S(△DEC) ;