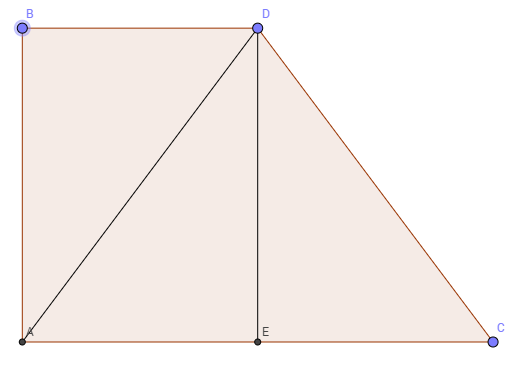
ADC - тең қабырғалы үшбұрыш;
ABD - тік бұрышты үшбұрыш;
AD = DC = CA = a;
ABC тең қабырғалы үшбұрышында B нүктесіен AC-ға биіктік түсірсек;
Дұрыс үшбұрыштың биіктігі - DE = √3 / 2 * a;
AB = DE = √3 / 2 * a;
ABD - тік бұрышты үшбұрышта Пифагор теоремасы бойынша:
AB^2 + BD^2 = AD^2;
(√3 / 2 * a) + BD^2 = a^2;
BD^2 = a^2 - 3/4 * a^2 = 1/4 * a^2;
BD = a/2;
Трапецияның орта сызығы = (AC + BD)/2 = (a + a/2) / 2 = 3a;