1. Есептің шартын түсіну:
Бізде дұрыс төртбұрышты призма берілген. Бұл дегеніміз, оның табаны квадрат, ал бүйір жақтары квадратқа перпендикуляр.
Табан қабырғасының ұзындығы 15 см.
Бүйір жағының диагоналі 25 см.
Бізге табан қабырғасынан призманың онымен қиылыспайтын диагоналіне дейінгі ең аз қашықтықты табу керек.
2. Сурет салу:
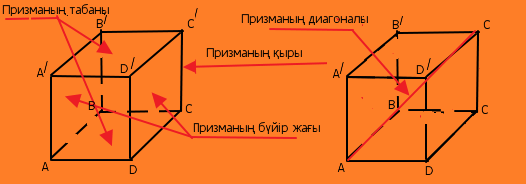
Суретте:
ABCD - призманың төменгі табаны
A'B'C'D' - призманың жоғарғы табаны
AA', BB', CC', DD' - призманың бүйір қырлары
AC' - призманың табан қабырғасымен қиылыспайтын диагоналі
3. Шешуі:
Призманың биіктігін табу:
Призманың бүйір жағы тіктөртбұрыш болғандықтан, Пифагор теоремасы бойынша бүйір қырын (призманың биіктігін) табамыз:
AA'² = AB² + A'B² AA'² = 15² + 25² = 850 AA' = √850 = 5√34 см
Ең аз қашықтықты табу:
Табан қабырғасынан (мысалы, AB) диагональға (AC') дейінгі ең аз қашықтық - бұл AB қабырғасынан A'C' түзуіне дейінгі перпендикулярдың ұзындығы.
A'C' түзуі AA'C' жазықтығында жатыр.
AB қабырғасы AA'C' жазықтығына параллель.
Сондықтан, AB-дан A'C' түзуіне дейінгі қашықтық A нүктесінен AA'C' жазықтығына дейінгі қашықтыққа тең.
A нүктесінен AA'C' жазықтығына дейінгі қашықтық AA'C' тікбұрышты үшбұрышының AA' катетіне түсірілген биіктікке тең.
Үшбұрыштың ауданын екі түрлі жолмен есептейік:
S(AA'C') = 1/2 * AA' * AC'
S(AA'C') = 1/2 * A'C' * h (мұндағы h - ізделінді қашықтық)
Бұл екі өрнекті теңестіріп, h табамыз: 1/2 * AA' * AC' = 1/2 * A'C' * h h = AA' * AC' / A'C' h = AA' * AC' / √(AA'² + AC²) h = 5√34 * 15 / √(850 + 15²) h = 75√34 / √1075 h = 75√34 / 5√43 h = 15√34 / √43 см
Жауабы: Табан қабырғасынан призманың онымен қиылыспайтын диагоналіне дейінгі ең аз қашықтық 15√34 / √43 см-ге тең.