Question

1.Көршілес екі қабырғасы 6см-ден, ал үлкен бұрышы 135градус болатын тік бұрышты трапецияның ауданын табындар.
2.Теңбүйірлі трапецияның табандары 24см және 40см, ал диагональдары өзара перпендикуляр. Трапецияның ауданын табыңдар.

Answer 1

АВСД - трапеция, ∠А=∠В=90°, АВ=ВС=6 см, ∠С=135°.

 Табу керек S-?

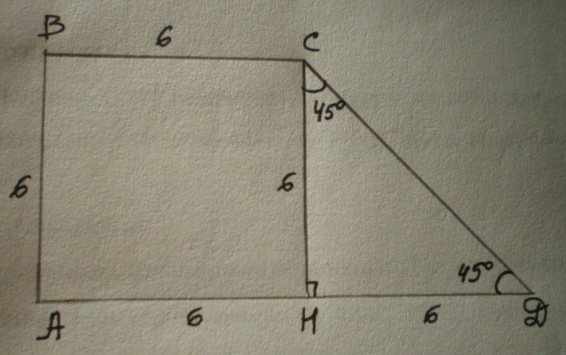
Шешуі: CH биіктігін сызып  ΔСДН -тікбұрышты үшбұрыш етіп қарастырамыз. ∠НСД=135-90=45°, сонда  ∠Д=45° тікбұрышты үшбұрыштың сүйір бұрыштарының қосындысының қасиеті бойынша). Бұрыштардың теңдігінен қабырғалардың теңдігі шығады, СН=ДН=6 см.

АН=ВС=6 см., АД=АН+ДН=6+6=12 см.

S=(АД+ВС)\2 * СН=(6+12)\2*6=54 см²

Жауабы: 54 см².

Answer 2

Егер тең қабырғалы трапецияның диагональдары өзара перпендикуляр болса, онда бұл трапецияның биіктігі трапецияның орта сызығына тең болады. Ортаңғы сызық: (24+40)/2=32(см) демек, биіктігі 32см. Трапецияның ауданы: ((24+40):2)*32=1024 кв.см.